[Zurück]

                                                                            Einige Gedanken zu Basel II.

I Ausgangspunkt.

Der seit 1974 existierende Basler Ausschuss für Bankenaufsicht hat in einem, im Jahr 2001 vorgelegten
Papier die Optimierung der Eigenkapitalabsicherung von Krediten vorgeschlagen. Nach diesem Vor-
schlag soll die 1988 beschlossene pauschale Eigenkapitalhinterlegung von 8% (Basel I) durch Berück-
sichtigung der Risiken der einzelnen Kredite an die jeweilige Situation angepaßt werden (Basel II).
Hiernach ergibt sich für die Banken die Notwendigkeit einer neuen Vergabepolitik und die Einkalku-
lation der speziellen Risiko-Kosten in den jeweiligen Kredit.

Hintergrund sind die in den letzten Jahren stark angestiegenen Wertberichtigungen der Banken für
faule Kredite. So mußte die HypoVereinsbank allein im Jahr 2001 ca. 2 Milliarden Euro für die
Risikovorsorge im Kreditgeschäft aufwenden [Prof. H. Schierenbeck; Basel II: Was ändert sich für
Banken und Kreditkunden; Uni Basel]. Dieses Kosten müssen in die Preispolitik des Kreditgeschäfts
Eingang finden. Wir wollen hier einmal - rein hypothetisch, versteht sich - der Frage nachgehen, was
wäre, wenn der Kreditnehmer den gesamten, wahrscheinlichen Ausfall seines Kredits mitfinanzieren
sollte, und zwar mit den Raten, die er anfänglich zu zahlen imstande ist.

Dazu gehen wir von folgendem Szenarium aus. Ein Kreditnehmer erhält von einem Kreditgeber eine
feste Kreditsumme K. Diese Kreditsumme ist je Zinsperiode mit einem festen Zinssatz z zu verzinsen.
Die Tilgung des Kredits erfolgt in gleichbleibenden Raten R über eine vorgegebene Laufzeit von L Zins-
perioden.

Nach üblicher Rechnung gilt (siehe Anhang, falls die Formel nicht so vertraut ist)

                                                    ,                                                             (1)

wobei q := 1 + z/100 den Kapitalisierungsfaktor darstellt.

Nun sei jedoch nicht sicher, daß der Kreditnehmer den Kredit über die gesamte Laufzeit L bedienen
kann, d.h in der Lage sein wird, die Raten wie vereinbart zurückzuzahlen. Damit entsteht für den Kre-
ditgeber ein Ausfallrisiko, das er in die Kreditkonditionen einkalkulieren muß. Dies kann zum Beispiel
darin bestehen, daß zur Kompensation des zu erwartenden Verlustes auf die Rate R ein Risikoaufschlag
A zu zahlen ist. Dies führt dementsprechend zu der erhöhten Rate R' = R + A. Dieser Rate R' entspricht
nach (1) ein erhöhter Zinssatz z', der im allgemeinen nur numerisch bestimmt werden kann (s.unten).

II Wahrscheinlichkeits - Modell.

Wir führen folgende Bezeichnungen ein:

K Kreditsumme
R Tilgungsrate
L Laufzeit (= Anzahl der zu zahlenden Tilgungsraten)
z Zinssatz
q Kapitalisierungsfaktor ( q := 1 + z/100)
N Anzahl der tatsächlich geleisteten Tilgungsraten.

Wir gehen davon aus, daß N eine Zufallsvariable ist, mit Verteilungsfunktion F(x) := P{N < x}.
Über F können zunächst nur folgende Aussagen gemacht werden.

1     F(x) = 0, für x < 0. Negative Tilgungsraten würde ja bedeuten, der Kreditnehmer bekommt
       die Tilgungsraten geschenkt, anstatt sie bezahlen zu müssen.

2     F(x) = 1, für x > L. Mehr wie L Tilgungsraten zahlt der Kreditnehmer natürlich nicht.

Zwischen x = 0 und x = L kennt man den Verlauf von F nicht. Daher muß man für diesen Be-
reich Modellannahmen machen. Zwei einfache Modelle sollen diskutiert werden.

1. Modell

Es ist durchaus sinnvoll, zunächst eine Gleichverteilung anzunehmen. Dies bedeutet praktisch,
daß der Kreditnehmer mit gleicher Wahrscheinlichkeit, während der gesamten Laufzeit des Kre-
dits, nach N < L geleisteten Tilgungsraten, die weiteren Zahlungen einstellt. Die Unabhängigkeit
dieser Wahrscheinlichkeit von N bedeutet praktisch, daß die Tatsache, daß der Kreditnehmer nach
und nach die Raten R zahlt, keinen Einfluß auf seine Zahlungsfähigkeit hat. Dies ist gerechtfertigt,
wenn der Kreditnehmer die Raten aus laufenden Einnahmen zahlt, und nicht etwa aus einem festen
Fonds, der keine Zuflüsse hat. In diesem Fall wäre es ja aber auch unsinnig einen Kredit aufzuneh-
men, da man das Geld ja schon auf der hohen Kante hat.

Für F(x) nehmen wir also folgenden Verlauf an. Hierbei ist P0 die Ausfallwahrscheinlichkeit des
Kredits, d.h. die Wahrscheinlichkeit, daß der Kreditnehmer nicht alle der L Raten zurückzahlen
kann. Somit ist F(x) = 0 für x < 0 und F(x) = 1 für x > L, und F(x) = P0 dazwischen.

                                                   (2)

Wenn also der Kreditnehmer nach N < L Zahlungen die weiteren Zahlungen einstellt , dann stellen
die restlichen L - N Zahlungen ein Verlustrisiko dar, das wie N ebenfalls eine Zufallsvariable V(x)
darstellt. Für diese gilt

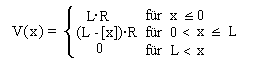                                        .                                         (3)

Hier ist x der Zeitparameter und [x] der ganze Teil von x. Daraus ergibt sich für den Erwartungswert
für die Zufallsvariable V(x)

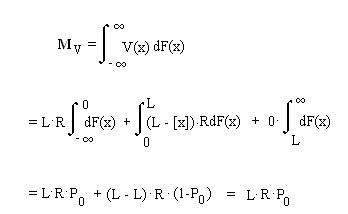                                ,                   (4)                               

da nur das (Stieltjes-) Integral in der Mitte an den Sprungstellen einen Beitrag liefert.

Ein reichlich triviales Ergebnis, das man auch hätte erraten können! Will man nun den Erwartungswert
von V als Risikoaufschlag auf die Tilgungsrate aufschlagen, so bekommt man eine Tilgungsrate R', mit

                                                           .

Hieraus ist ersichtlich, daß bei diesem Modell der Risikoaufschlag unabhängig von der Laufzeit ist.
Es gibt leider keine einfache Formel, um den entsprechenden Zinssatz z' zu der Tilgungsrate R' zu be-
stimmen. Mit q' := (1 + z'/100) gilt aber

                                                    ,                         (5)

wie aus (1) ersichtlich ist.

Um aber ein gewisses Gefühl für die Änderung der Zinssätze zu bekommen, kann man aus (5) den
Ausdruck

                                                                     (6)

bilden. Hieraus kann man numerisch durch Einsetzen der Werte von L, z und z' die zugehörigen Risiko-
wahrscheinlichkeiten P0 ermitteln. In der folgenden Tabelle sollen exemplarisch einige dieser Werte näher
betrachtet werden.

In den Tabelleneinträgen sind die Ausfallwahrscheinlichkeiten P0 angegeben, wobei in den Zeilen
die Werte für gleichen Ausgangszinssatz z stehen, und in den Spalten die Werte für gleichen er-
höhten Zinssatz z'.

Man sieht hieraus:

1     Ein ähnliches Ausfallrisiko erzeugt bei kurzen Laufzeiten einen deutlich höheren Zinsaufschlag,
       als bei längeren Laufzeiten. Geht man nämlich in einer Zeile horizontal weiter, dann sieht man,
       daß die Risiken bei einer Laufzeit von 20 Perioden deutlich höher sein müssen, um den gleichen
       erhöhten Zinssatz zu erzeugen, wie bei einer Laufzeit von 10.

       Dies entspricht jedoch nicht immer der gängigen Praxis. Häufig werden bei längerfristigen Kre-
       diten höhere Zinsen veranschlagt, wie bei kurzfristigen.

2     Die Tabelleneinträge parallel zur Diagonalen fallen in Richtung des größeren Ausgangszins z.
       Dies bedeutet, daß bei höherem Ausgangszinssatz bereits ein geringeres Risiko zu einem er-
       höhten Zinssatz z' führt, was natürlich logisch ist. Dies gilt sowohl für kurze, als auch für lange
       Laufzeiten.

Natürlich könnte man z' aus gegebenen L, z und P0 mit einem geeigneten Algorithmus numerisch be-
stimmen, wir wollen es aber bei den obigen Betrachtungen belassen.

2. Modell.

Man kann zum Beispiel auch annehmen, daß der Kreditnehmer stille Reserven hat, die es ihm erlau-
ben, den Kredit dann immer noch eine gewisse Zeit zu bedienen, wenn er es aus seinen laufenden Ein-
nahmen nicht mehr kann. Zum Beispiel könnte es sein, daß er einige Wertgegenstände hat, die er im
Fall eines Liquiditätsengpasses - gegebenenfalls mit Verlust - veräußern könnte. Diese Wertgegen-
stände wären dann für den Kreditgeber eine Art Sicherheit, daß für den Fall der Zahlungsunfähigkeit
des Kreditnehmers noch eine gewisse Anzahl von Tilgungsraten bezahlt werden könnten.

Sei k die Anzahl der Raten, die durch die Sicherheit mit Wert W beglichen werden könnten. So daß
also gilt kR W (k+1)R. Wir setzen L' := L - k. Damit ergibt sich für die Verteilungsfunktion F(x)
der folgende Verlauf

                                .

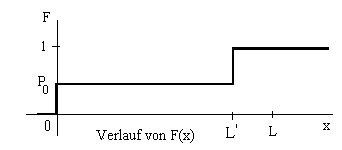Dies heißt, daß wenn der Kreditnehmer L' Raten bezahlt hat, dann kann der Kredit voll bedient werden,
auch wenn der Kreditnehmer danach zahlungsunfähig wird. Lediglich die ersten L' Raten sind unsicher.
Für die Zufallsvariable V(x), die das Ausfallrisiko darstellt gilt in diesem Fall

                                                  .

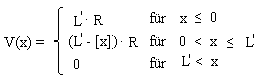Für den Mittelwert erhält man

Wiederum ein reichlich triviales Ergebnis, das man ebenso hätte erraten können. Es zeigt, daß man bei
der Kreditvergabe den Veräußerungsgewinn der Sicherheiten schätzen muß, dann die Anzahl der Til-
gungsraten zu bestimmen hat, die damit gezahlt werden können, um dann die Laufzeit um diese Anzahl
zu kürzen. Mit der daraus resultierenden fiktiven Laufzeit L' geht dann die Rechnung wie in Modell 1.

Beide vorstehenden Modelle setzen selbstverständlich voraus, daß das Risiko eines Ausfalls nicht
von der Höhe der Raten abhängt!

III Anhang

1. Zu Formel (1).

Den Verlauf der Zahlungsrückflüsse kann man wie folgt notieren

Ende der Periode Zinsen Restschuld
1                         Kq                 S1 = Kq - R
2                         S1q                S2 = S1q - R = Kq² - Rq - R
...                         ...                   ...
n                         S(n-1)q           Sn= Kq - Rq - Rq -...- Rq

Hieraus und aus der Forderung Sn = 0 ergibt sich (1) für n = L.

2.

Zur Diskussion der Formeln (5) und (6) kann man die Funktion F(q,L) betrachten, mit

Hieraus ergibt sich z.B.

                                        ,

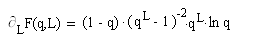und daraus für 1 q, daß

                                                       .

Hieraus sieht man mit (1) , daß die Rate R bei gleicher Kreditsumme und gleichem Zinssatz mit wachsen-
dem L abnimmt. Man hüte sich aber vor dem üblichen Slogan "bequeme Raten, lange Laufzeit". Die Zins-
summe (nicht der Zinssatz) wächst mit L stark an!